Potencial eléctrico
El potencial eléctrico en un punto es el trabajo que debe realizar un campo electrostático para mover una carga positiva q desde el punto de referencia, dividido por unidad de carga de prueba. Dicho de otra forma, es el trabajo que debe realizar una fuerza externa para traer una carga unitaria q desde la referencia hasta el punto considerado en contra de la fuerza eléctrica. Matemáticamente se expresa por:
Trabajo eléctrico y energía potencial eléctrica
Considérese una carga puntual en presencia de un campo eléctrico
en presencia de un campo eléctrico  cualquiera. La carga experimentará una fuerza eléctrica:
cualquiera. La carga experimentará una fuerza eléctrica:
 la fuerza eléctrica hará un trabajo diferencial
la fuerza eléctrica hará un trabajo diferencial  expresado como:
expresado como:
 que recorre una determinada trayectoria A - B en las inmediaciones de una carga
que recorre una determinada trayectoria A - B en las inmediaciones de una carga 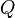 tal y como muestra la figura 1. Siendo
tal y como muestra la figura 1. Siendo  el desplazamiento infinitesimal de la carga
el desplazamiento infinitesimal de la carga  en la dirección radial, el trabajo diferencial
en la dirección radial, el trabajo diferencial  se puede expresar así:
se puede expresar así:
 de la carga
de la carga 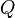 y la posición final B, distante
y la posición final B, distante  de la carga
de la carga 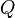 :
:
 no depende de la trayectoria seguida por la partícula, sólo depende de la posición inicial y final, lo cual implica que la fuerza eléctrica
no depende de la trayectoria seguida por la partícula, sólo depende de la posición inicial y final, lo cual implica que la fuerza eléctrica  es una fuerza conservativa. Por lo tanto se puede definir una energía potencial que permite calcular el trabajo más fácilmente:
es una fuerza conservativa. Por lo tanto se puede definir una energía potencial que permite calcular el trabajo más fácilmente:
Por convención, el nivel cero de energía potencial se suele establecer en el infinito, es decir, si y sólo si .
.
Campo eléctrico uniforme
Sean A y B dos puntos situados en un campo eléctrico uniforme, estando A a una distancia d de B en la dirección del campo, tal como muestra la figura.
Considérese una carga de prueba positiva q moviéndose sin aceleración, por efecto de algún agente externo, siguiendo la recta que une A con B.
La fuerza eléctrica sobre la carga será qE y apunta hacia abajo. Para mover la carga en la forma descrita arriba, se debe contrarrestar esa fuerza aplicando una fuerza externa F de la misma magnitud pero dirigida hacia arriba. El trabajo realizado por el agente que proporciona esta fuerza es:
realizado por el agente que proporciona esta fuerza es:



El punto B tiene un potencial más elevado que el A. Esto es razonable porque un agente exterior tendría que hacer trabajo positivo para mover la carga de prueba de A hacia B.
 sobre la carga de prueba, tal como se ve en la figura. Para evitar que la carga acelere, debe aplicarse una fuerza
sobre la carga de prueba, tal como se ve en la figura. Para evitar que la carga acelere, debe aplicarse una fuerza  que sea exactamente igual a
que sea exactamente igual a  para todas las posiciones del cuerpo de prueba.
para todas las posiciones del cuerpo de prueba.
Si el agente externo hace que el cuerpo de prueba se mueva siguiendo un corrimiento a lo largo de la trayectoria de A a B, el elemento de trabajo desarrollado por el agente externo es
a lo largo de la trayectoria de A a B, el elemento de trabajo desarrollado por el agente externo es  . Para obtener el trabajo total
. Para obtener el trabajo total  hecho por el agente externo al mover la carga de A a B, se suman las contribuciones al trabajo de todos los segmentos infinitesimales en que se ha dividido la trayectoria. Así se obtiene:
hecho por el agente externo al mover la carga de A a B, se suman las contribuciones al trabajo de todos los segmentos infinitesimales en que se ha dividido la trayectoria. Así se obtiene:

 , al sustituir en esta expresión, se obtiene que
, al sustituir en esta expresión, se obtiene que

 al infinito toma el valor de cero, esta ecuación da el potencial en el punto B, o bien, eliminando el subíndice B,
al infinito toma el valor de cero, esta ecuación da el potencial en el punto B, o bien, eliminando el subíndice B,
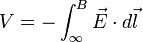
 .
.
El potencial eléctrico sólo se puede definir para un campo estático producido por cargas que ocupan una región finita del espacio. Para cargas en movimiento debe recurrirse a los potenciales de Liénard-Wiechert para representar un campo electromagnético que además incorpore el efecto de retardo, ya que las perturbaciones del campo eléctrico no se pueden propagar más rápido que la velocidad de la luz. Si se considera que las cargas están fuera de dicho campo, la carga no cuenta con energía y el potencial eléctrico equivale al trabajo necesario para llevar la carga desde el exterior del campo hasta el punto considerado. La unidad del sistema internacional es el voltio(V). Todos los puntos de un campo eléctrico que tienen el mismo potencial forman una superficie equipotencial.
Trabajo eléctrico y energía potencial eléctrica
Considérese una carga puntual
 en presencia de un campo eléctrico
en presencia de un campo eléctrico  cualquiera. La carga experimentará una fuerza eléctrica:
cualquiera. La carga experimentará una fuerza eléctrica:(1)Esta fuerza realizará un trabajo para trasladar la carga de un punto A a otro B, de tal forma que para producir un pequeño desplazamiento
 la fuerza eléctrica hará un trabajo diferencial
la fuerza eléctrica hará un trabajo diferencial  expresado como:
expresado como:(2)Teniendo en cuenta la expresión ():
(3)Por lo tanto, integrando obtenemos que el trabajo total realizado por el campo eléctrico será:
(4)En un caso concreto con un campo eléctrico definido: Sea una carga puntual
 que recorre una determinada trayectoria A - B en las inmediaciones de una carga
que recorre una determinada trayectoria A - B en las inmediaciones de una carga 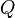 tal y como muestra la figura 1. Siendo
tal y como muestra la figura 1. Siendo  el desplazamiento infinitesimal de la carga
el desplazamiento infinitesimal de la carga  en la dirección radial, el trabajo diferencial
en la dirección radial, el trabajo diferencial  se puede expresar así:
se puede expresar así:(5)Para calcular el trabajo total, se integra entre la posición inicial A, distante
 de la carga
de la carga 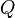 y la posición final B, distante
y la posición final B, distante  de la carga
de la carga 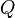 :
:(6)De la expresión () se concluye que el trabajo
 no depende de la trayectoria seguida por la partícula, sólo depende de la posición inicial y final, lo cual implica que la fuerza eléctrica
no depende de la trayectoria seguida por la partícula, sólo depende de la posición inicial y final, lo cual implica que la fuerza eléctrica  es una fuerza conservativa. Por lo tanto se puede definir una energía potencial que permite calcular el trabajo más fácilmente:
es una fuerza conservativa. Por lo tanto se puede definir una energía potencial que permite calcular el trabajo más fácilmente:(7)El trabajo realizado por la fuerza eléctrica para desplazar una partícula entre A y B será:
(8)
Por convención, el nivel cero de energía potencial se suele establecer en el infinito, es decir, si y sólo si
 .
.Campo eléctrico uniforme
Sean A y B dos puntos situados en un campo eléctrico uniforme, estando A a una distancia d de B en la dirección del campo, tal como muestra la figura.
La fuerza eléctrica sobre la carga será qE y apunta hacia abajo. Para mover la carga en la forma descrita arriba, se debe contrarrestar esa fuerza aplicando una fuerza externa F de la misma magnitud pero dirigida hacia arriba. El trabajo
 realizado por el agente que proporciona esta fuerza es:
realizado por el agente que proporciona esta fuerza es:


El punto B tiene un potencial más elevado que el A. Esto es razonable porque un agente exterior tendría que hacer trabajo positivo para mover la carga de prueba de A hacia B.
Campo eléctrico no uniforme
En el caso más general de un campo eléctrico no uniforme, este ejerce una fuerza sobre la carga de prueba, tal como se ve en la figura. Para evitar que la carga acelere, debe aplicarse una fuerza
sobre la carga de prueba, tal como se ve en la figura. Para evitar que la carga acelere, debe aplicarse una fuerza  que sea exactamente igual a
que sea exactamente igual a  para todas las posiciones del cuerpo de prueba.
para todas las posiciones del cuerpo de prueba.Si el agente externo hace que el cuerpo de prueba se mueva siguiendo un corrimiento
 a lo largo de la trayectoria de A a B, el elemento de trabajo desarrollado por el agente externo es
a lo largo de la trayectoria de A a B, el elemento de trabajo desarrollado por el agente externo es  . Para obtener el trabajo total
. Para obtener el trabajo total  hecho por el agente externo al mover la carga de A a B, se suman las contribuciones al trabajo de todos los segmentos infinitesimales en que se ha dividido la trayectoria. Así se obtiene:
hecho por el agente externo al mover la carga de A a B, se suman las contribuciones al trabajo de todos los segmentos infinitesimales en que se ha dividido la trayectoria. Así se obtiene:
 , al sustituir en esta expresión, se obtiene que
, al sustituir en esta expresión, se obtiene que
 al infinito toma el valor de cero, esta ecuación da el potencial en el punto B, o bien, eliminando el subíndice B,
al infinito toma el valor de cero, esta ecuación da el potencial en el punto B, o bien, eliminando el subíndice B,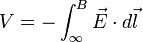
 .
.



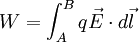

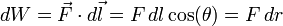


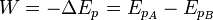
No hay comentarios:
Publicar un comentario